EMDE Illustrated
EMDE – motivations, explanations and intuitions
In this article we provide some intuitive explanations of our objectives and theoretical background of the Efficient Manifold Density Estimator (EMDE). We describe our inspirations and thought process which led to the formulation of the algorithm. Then, we dive further into technicalities to show how the intuitions link to actual mathematical formulas behind the algorithm.
Research on the EMDE algorithm started from spotting several shortcomings of current machine learning methods. Let us consider an extremely basic cognitive ability to group similar objects regardless of their individual differences. Even young children can group different pictures of elephants together and recognize that a giraffe doesn’t belong to this group. These kinds of abilities are shown even in the behavior of 10-month-old infants. It is not only a very basic skill but also a very important one for other more complex processes. It allows to organize perception and cognition in a changing environment. By analogy to human cognition, we wanted to create an algorithm that would be able to solve this task in a simple way without a disproportionate computational overhead, i.e., with a single linear pass, without quadratic computational complexity.

Looking at this from a slightly different angle: we wanted to aggregate various sets of vectors in a compressed representation, that can model membership function – recreate groupings created by object/event features represented by vectors. We were inspired by two algorithms: Count-Min Sketch (CMS) and Locality Sensitive Hashing. CMS is a very efficient algorithm used to approximate the number of occurrences of a given item in a data stream. The item count is incremented in multiple rows of a two-dimensional array (the sketch), where each row corresponds to a different hashing function. Then the minimum value for a given item across all hashing functions is an item count approximation. Using multiple hashing functions minimizes hash collisions impact. While CMS applies random hashes to item labels, LSH aims to put in the same bucket items that are close together in the input space. EMDE borrowed the idea of histogram-like count over many hashing functions from CMS and from LSH a space hashing approach that is aware of the input space geometry.
To understand the notion of input space geometry we need to introduce the concept of a data manifold. Formally speaking, a Riemannian manifold is a metric space that locally resembles Euclidean space near each point. The familiar Euclidean space itself is in fact a basic example of a manifold. When we consider vectors representing some aspect of objects we want to aggregate, for example image embeddings, all our data points represented by these embeddings can be seen as points on a manifold. The closeness of two points on a manifold will represent the similarity of objects in real-life with respect to the features expressed by vectors spanning the manifold. To aggregate some subset of data points, e.g. purchase history of a given user, we can represent it with a heatmap created over the manifold.
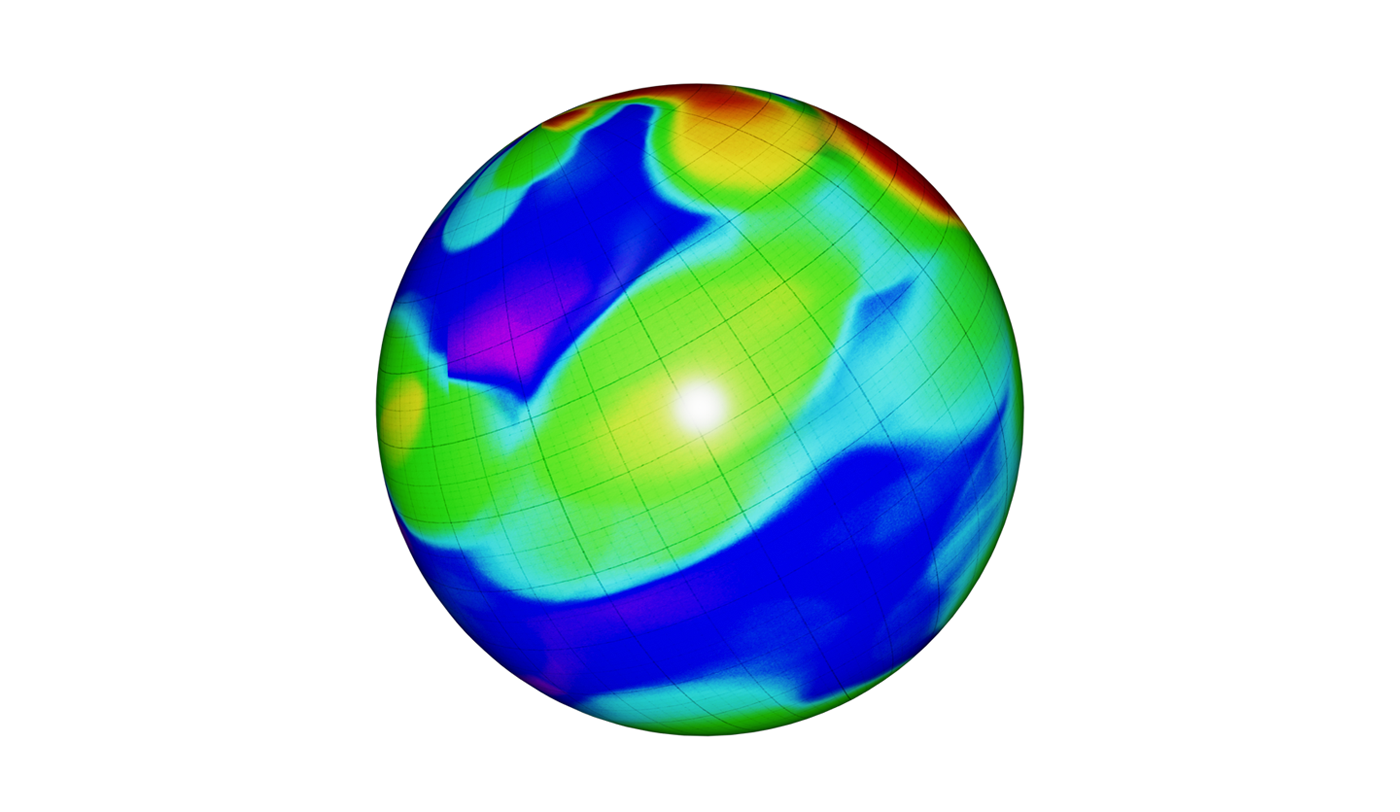
To develop some intuitive understanding behind this idea, let’s consider a manifold example that we can easily put our finger on – the Earth’s surface. Imagine a scenario in which we want to present information about places that a person visits and how often they visit these places. We could take a sphere representing the surface of the Earth and mark visited places with a heatmap. The lighter regions will represent places that are visited more often, and the darker regions places rarely visited or not visited at all.
Similar to the Earth surface, we can consider a manifold that is spanned by our image embeddings. It is important to note that the manifold is embedded in Rn, but is not the full Rn space. Image embeddings for all possible “images in the wild” will carve out a tiny fragment of Rn, and that fragment is our manifold of interest. We can, for example, create a heatmap where vectors representing products bought by a given user can be interpreted as “visited places” on a manifold. This heatmap will then inform us what kind of products (as described by their visual features) the user preferred in the past. If I bought many pairs of shoes and didn’t buy any swimwear, the region where shoe images reside will be brighter and the swimwear region will be completely dark. This way we can create accurate maps of user preferences.
However, we don’t need to limit ourselves to image embeddings, we can consider any type of vector representation as textual embeddings of product descriptions or user-product interaction vectors. By combining these sources of information, we can create really accurate models of user behavior. What is more, aggregating input in the form of heatmaps enables us to represent probability distributions, which is impossible when we use pointwise averages, or sequential inputs. So, the question of how to pass these maps over manifolds to a machine learning algorithm becomes crucial in our research. Also, when we consider a model output, we can represent it as a heatmap, for example expressing the probability of the next bought item. Recommendation task can be then stated as finding the right mapping between these two heatmaps – the user behavioral model and the probability of a next bought item. The question remains how to transfer information from the manifold to the finite-size data structure.
From manifold to sketch
The closeness of two points on the manifold informs us that two objects are similar with respect to features encoded in vector representations spanning the manifold. Taking this fact into consideration we could divide manifold into regions and treat the vectors falling into the same region as representations of objects of one kind. Then we would simply add up vectors in each region to transform information from a manifold into a numerical structure.
Going back to the heatmap of visited places– how can we transform it into a numerical matrix? We can make use of the fact that our globe is already divided into regions. For instance, we may count how many times a person was in a given country. But what if we have data from one month and want to observe someone’s day to day patterns? We can then go to the lower levels, like regions, cities, districts, etc. However, the finer division we assume the higher the number of regions is and thus we end up with a very big and hard-to-process structure.
Similarly, we need to divide the manifold into regions, which will allow us to create an accurate representation of an aggregated data heatmap. At the same time, the representation needs to be compact and easy to use as a part of a machine learning pipeline.
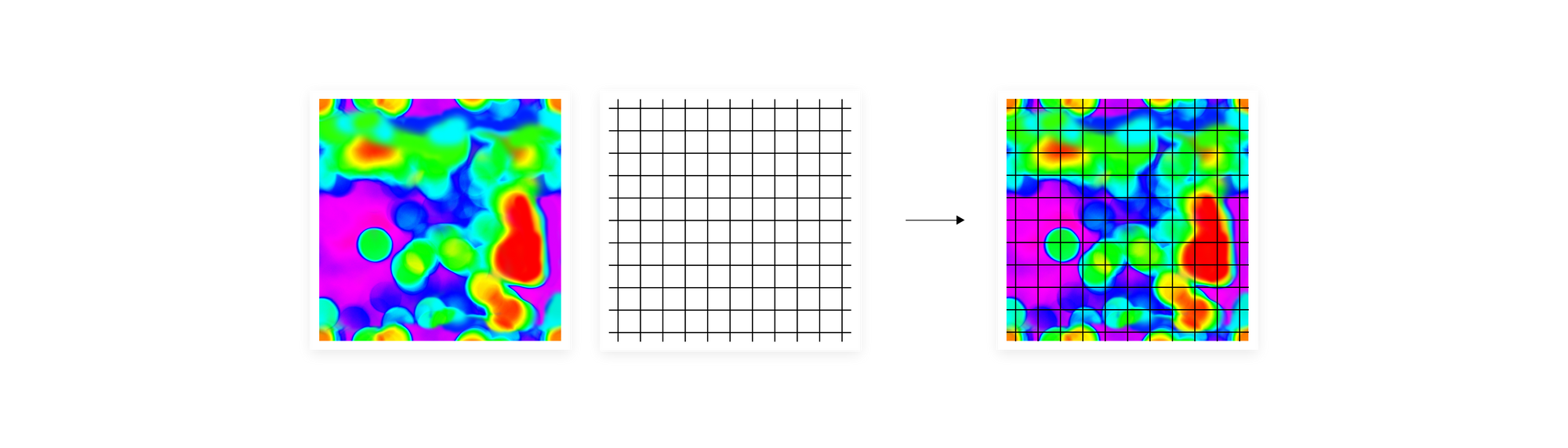
One solution will be to create an even grid over the heatmap and add up the vectors from each region. However, if we made the grid too coarse, we would lose some pieces of information we wanted to transfer from the manifold. Also, this kind of division will result in rather noisy categories, where objects of different kinds will often fall into the same region. On the other hand, by making a grid too fine-grained we end up with a huge matrix, extremely hard to process. It may also lack generalization, which was the point of aggregating vectors based on their closeness in the input space geometry, instead of passing them to the algorithm sequentially.
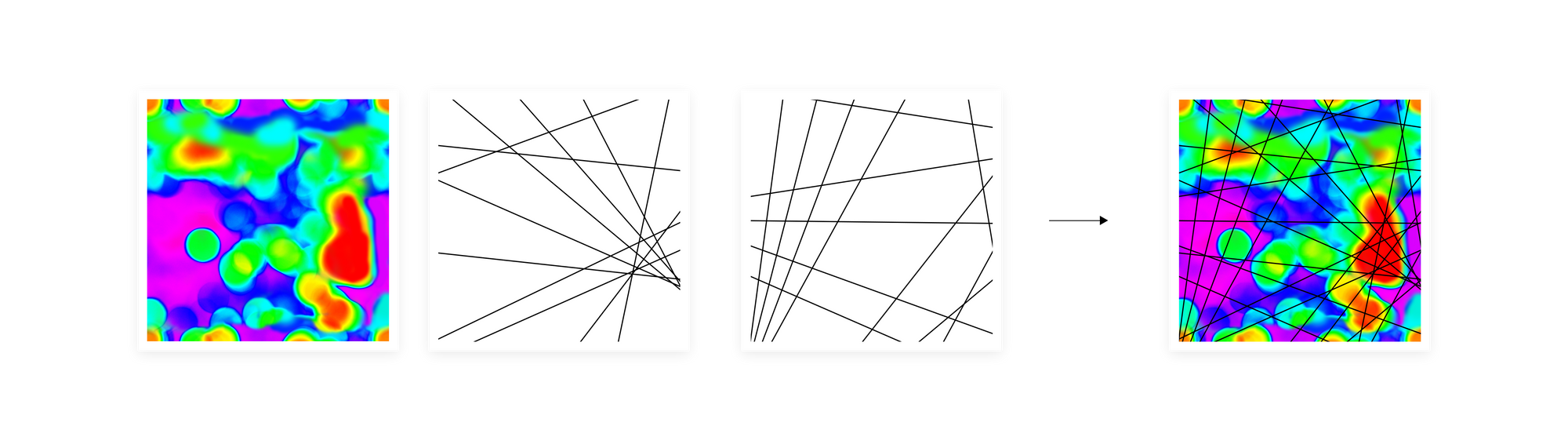
To overcome these obstacles, we create multiple independent manifold divisions. When we create two different grids and stack one on top of another, performing a geometric intersection, the number of regions that were created on the intersection of these two grids is much bigger than if we simply add up the number of regions from both grids. The larger the dimensionality of the original input space, the more subregions an intersection can give, with the upper bound being exponential with respect to the number of different divisions. Usually, embeddings used in machine learning as an input data representation are high-dimensional vectors so with the right number of separate manifold divisions, we can obtain a very high-resolution representation of a manifold. In a sense, we translate the heatmap drawn over the manifold into this kind of histogram on steroids. At the same time, we keep the final representation, a sketch, rather compact. Its width is defined by the number of regions in a single manifold division and depth is the number of separate divisions. The example size of a sketch used in our experiments is width 128 and depth 100.
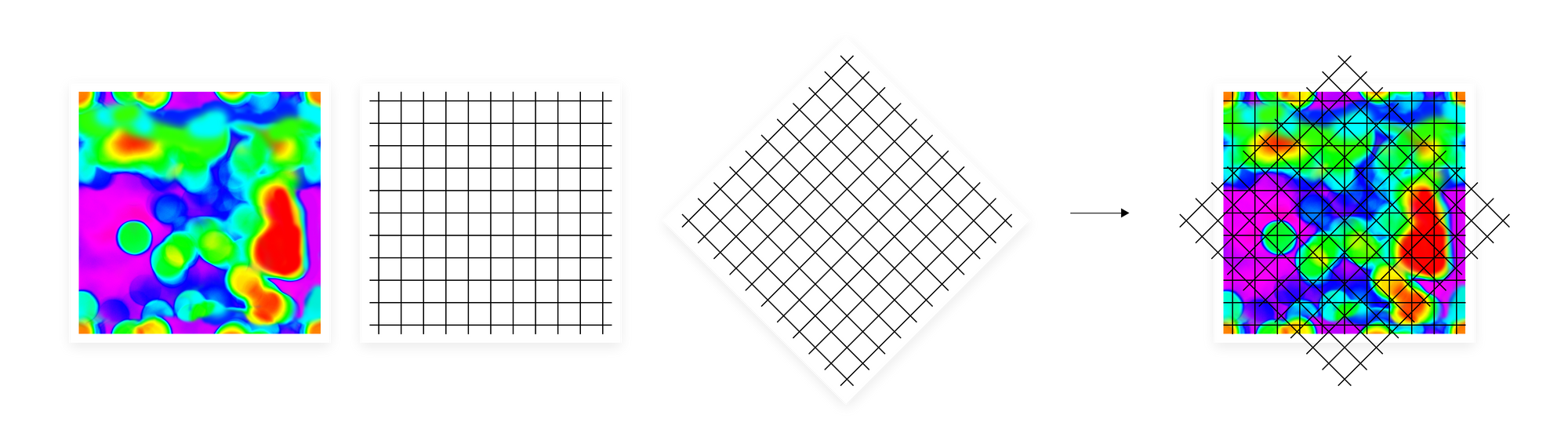
However, dividing the manifold with an even grid can result in many empty regions or all data points falling into one region. To prevent this, we use the quantile function when creating the hyperplanes dividing the manifold. This way we make sure that we divide manifold into non-empty regions in a density-dependent way.
Thus far we have provided some intuitive explanations of EMDE’s background. In the next section, we will present a step-by-step explanation of the algorithm itself and show how it can be used for model training and inference.
EMDE Step-by-step
Input data: vectors representing a given aspect of items we want to aggregate, e.g. embedding vectors of product descriptions, or Cleora embeddings (github repository) from behavioral user data
Manifold Partitioning
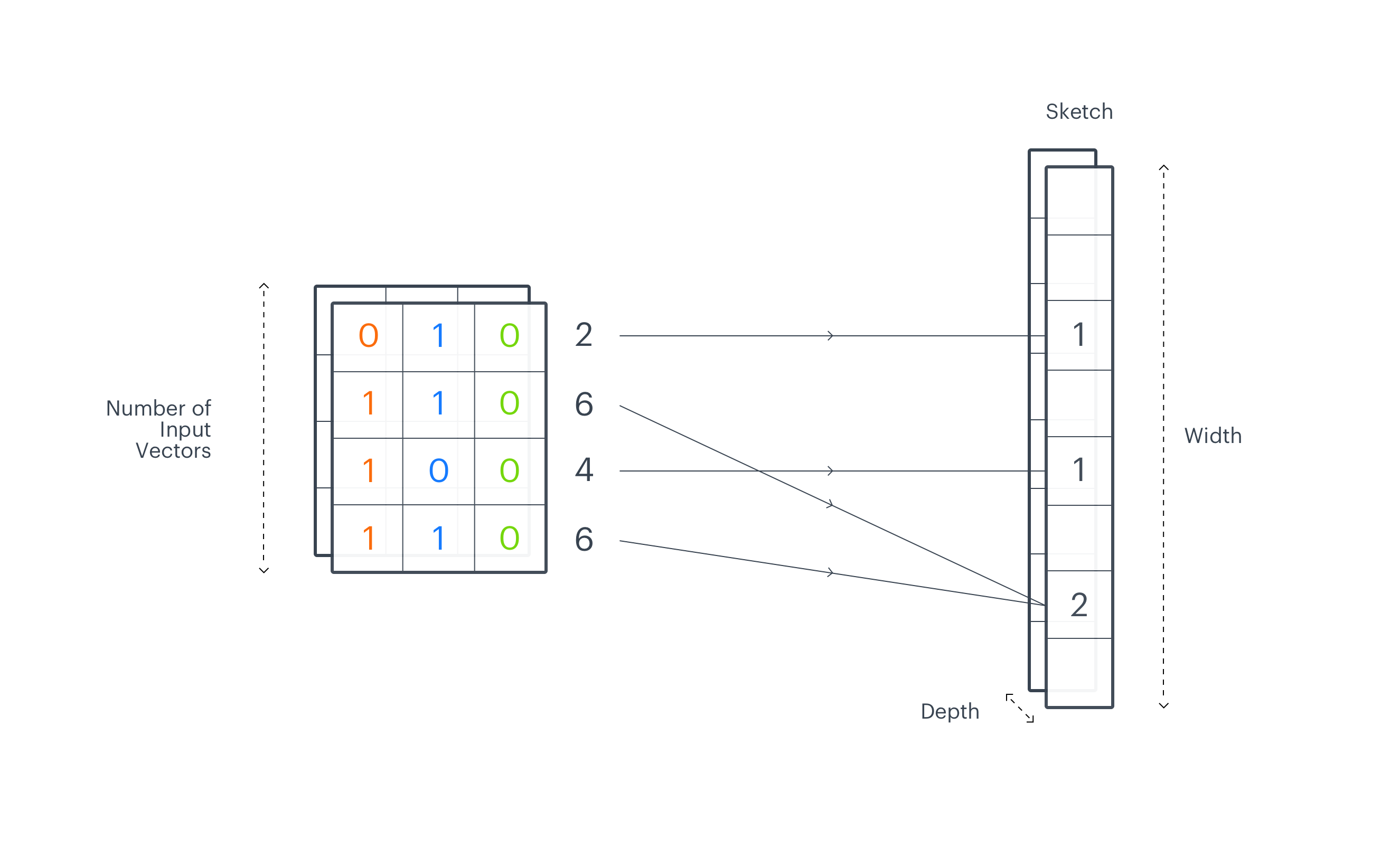
The central part of the EMDE algorithm is the data manifold partitioning procedure. First, K hyperplanes are selected to cut the manifold into 2K regions, and each region corresponds to one bucket in the final sketch. This makes the sketch_width dimension.
As each hyperplane divides manifold into two parts, we have K binary hash codes for a single input vector, which taken together represent the region that the vector falls into.
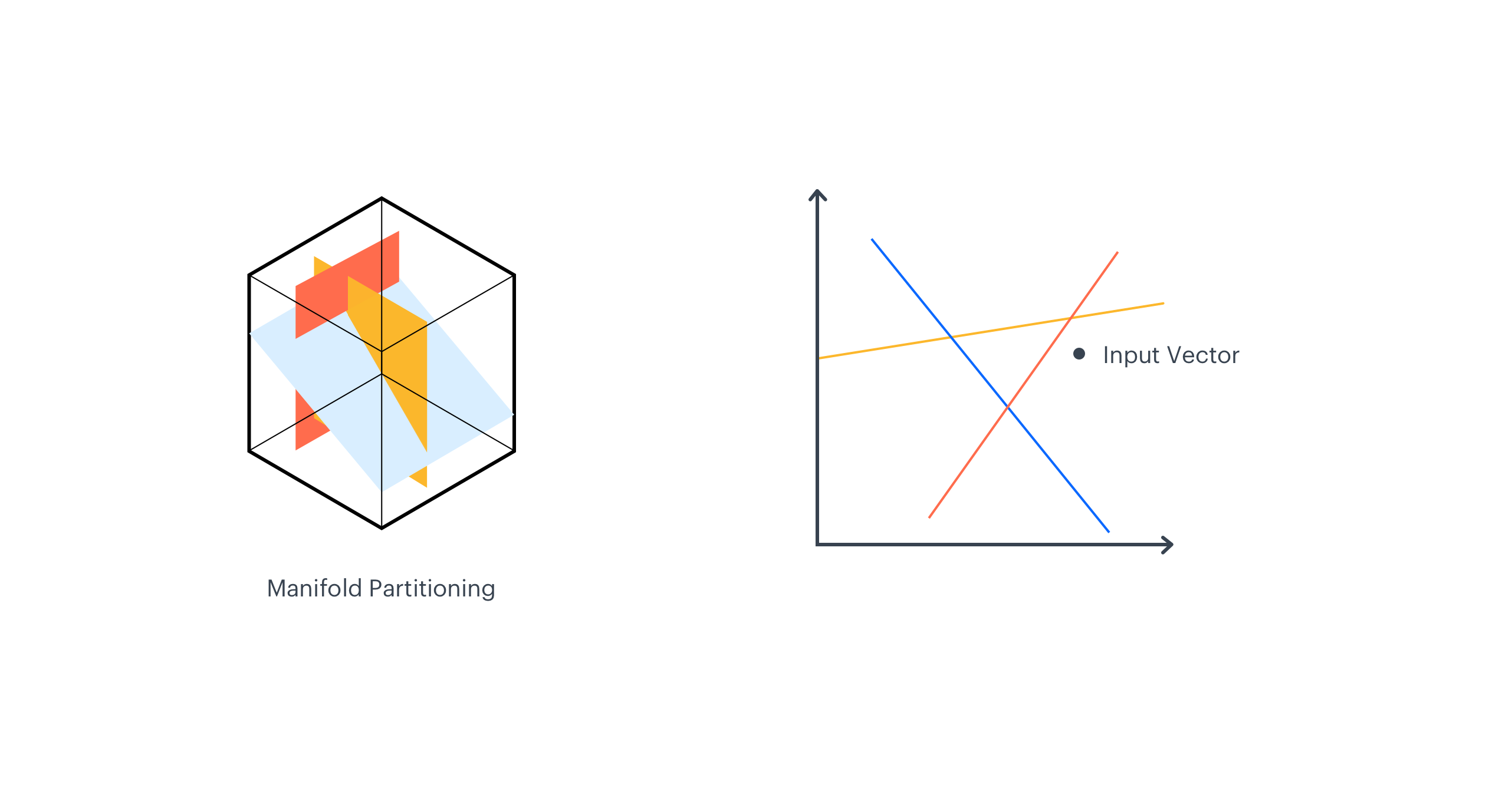
Hyperplane Selection
To avoid unutilized regions we want to cut the manifold into nonempty parts. To do so, we introduce the modified version of the LSH algorithm – Density-depended LSH. We generate K random vectors ri and calculate hash codes with the provided formula:
hashi(v) = sgn(v · ri −bi)
where v represents the input vector and bi is a bias drawn from the data-dependent quantile function of v · ri
Adding Depth
In the previous paragraph, we described how to create a single manifold division. In order to obtain a high-resolution representation, we need to create multiple independent divisions of a manifold. They will make the sketch_depth parameter. One independent partition creates 2K regions and each vector on a manifold falls into one of these regions. Next, we repeat manifold partitioning procedure, which results in creating different 2K regions. In this case, we end up with two binary vectors of a length K, each representing a region that a vector falls into in a given manifold division. We stack them together across the sketch_depth axis. Normally, the number of independent manifold divisions is higher. We can then assume that two similar vectors will often fall into the same region in different partitions.
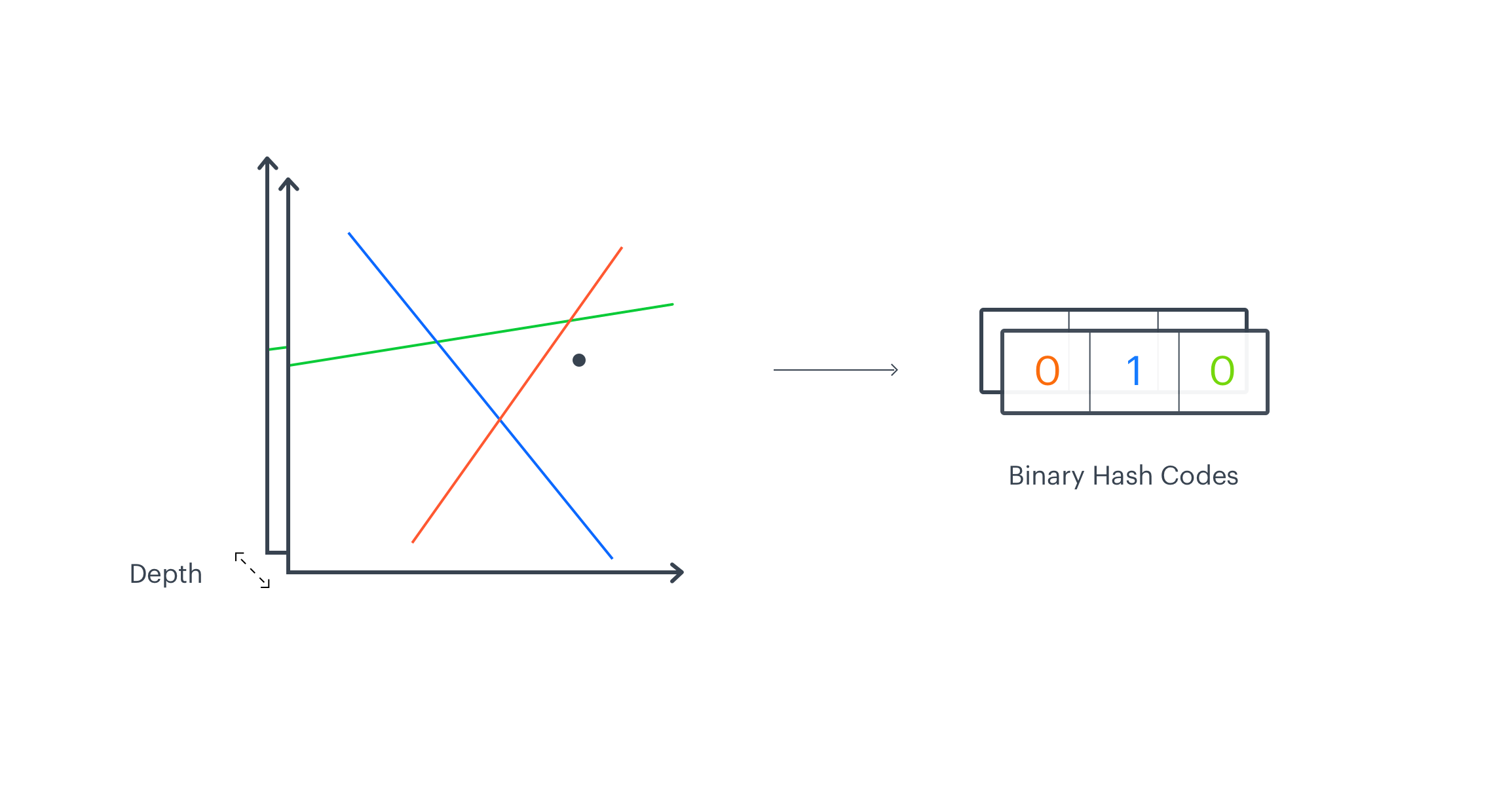
Sketches
The output of the EMDE algorithm is a sketch, an aggregated representation where each bucket stores the number of input vectors that fall into a particular region. Binary vectors calculated for all input embeddings are packed into integers we call codes. Codes represent the regions from the manifold division and indicate on which index of the final sketch to increment the count. This way we end up with an aggregated representation of input data. The described procedure is repeated separately on each depth-level. The final representation has two dimensions sketch_width – the number of regions from single manifold division (with K hyperplanes) and sketch_depth – the number of independent manifold divisions into sketch_width regions. To create a more robust representation we can concatenate sketches from different modalities like text, image, graphs.
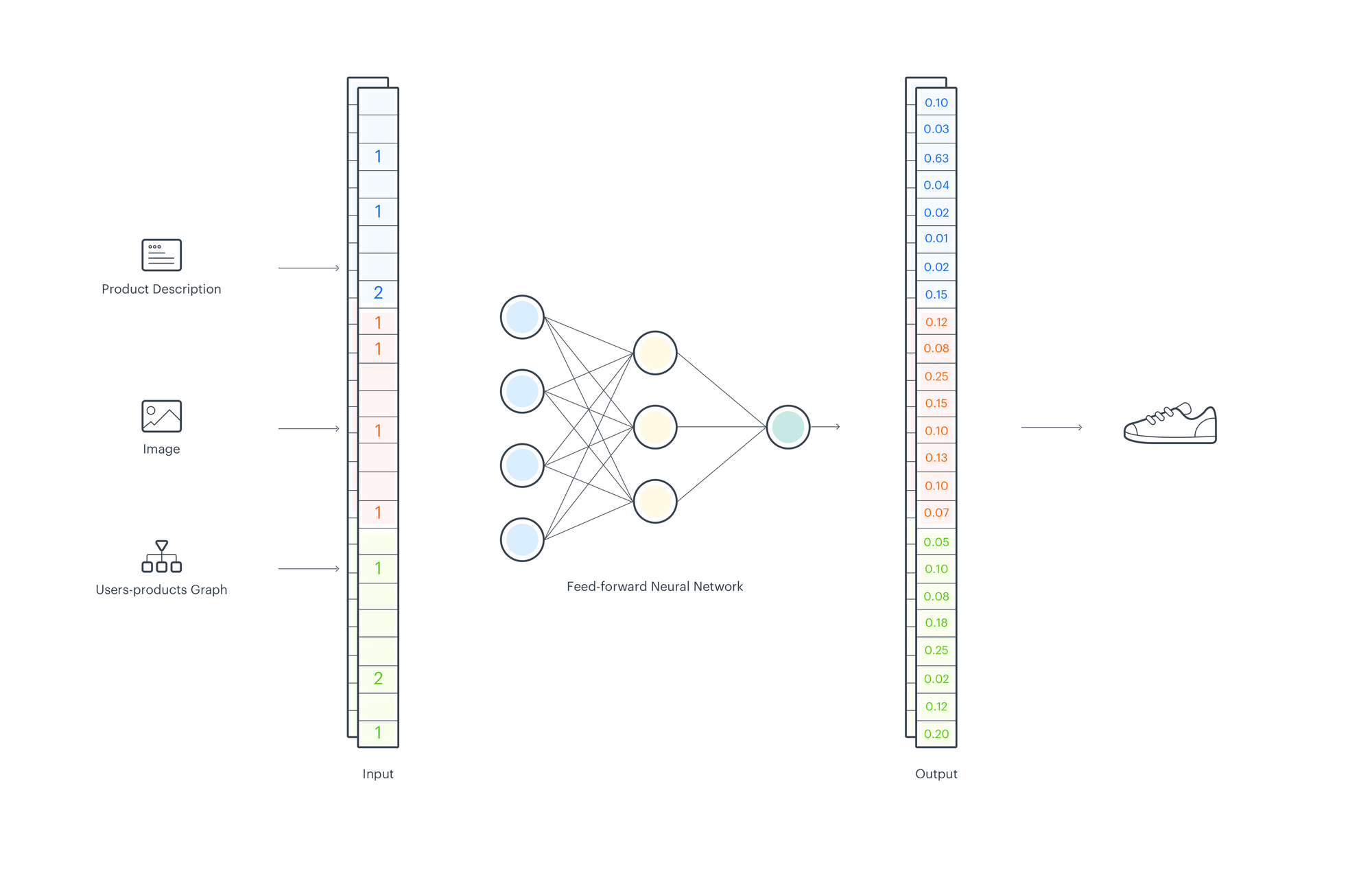
Using EMDE for Recommendations
From the previous part we know how to use EMDE to create aggregated data representation, now let’s consider how to train a recommender system using EMDE sketches. Based on user purchase history we want to predict the next items the user will buy. To create sketches, we use product descriptions, pictures, and user-product interaction graph. We can use one of the popular embedding methods for text and images. To create node embeddings, we use our own model Cleora, but any other graph embedding method can be also used with EMDE. For each input type, we create sketches separately and concatenate them.
To train a model we take purchase histories of many users. For each user, we aggregate events before a time split to create an input sketch and after the time split to create the target sketch – the purchases we want to predict. Data prepared this way are used to train a simple feed-forward neural network. The goal of training is to find the right mapping between the manifold regions that represents user past behavior/preferences to the manifold regions that represent the most probable next choices.
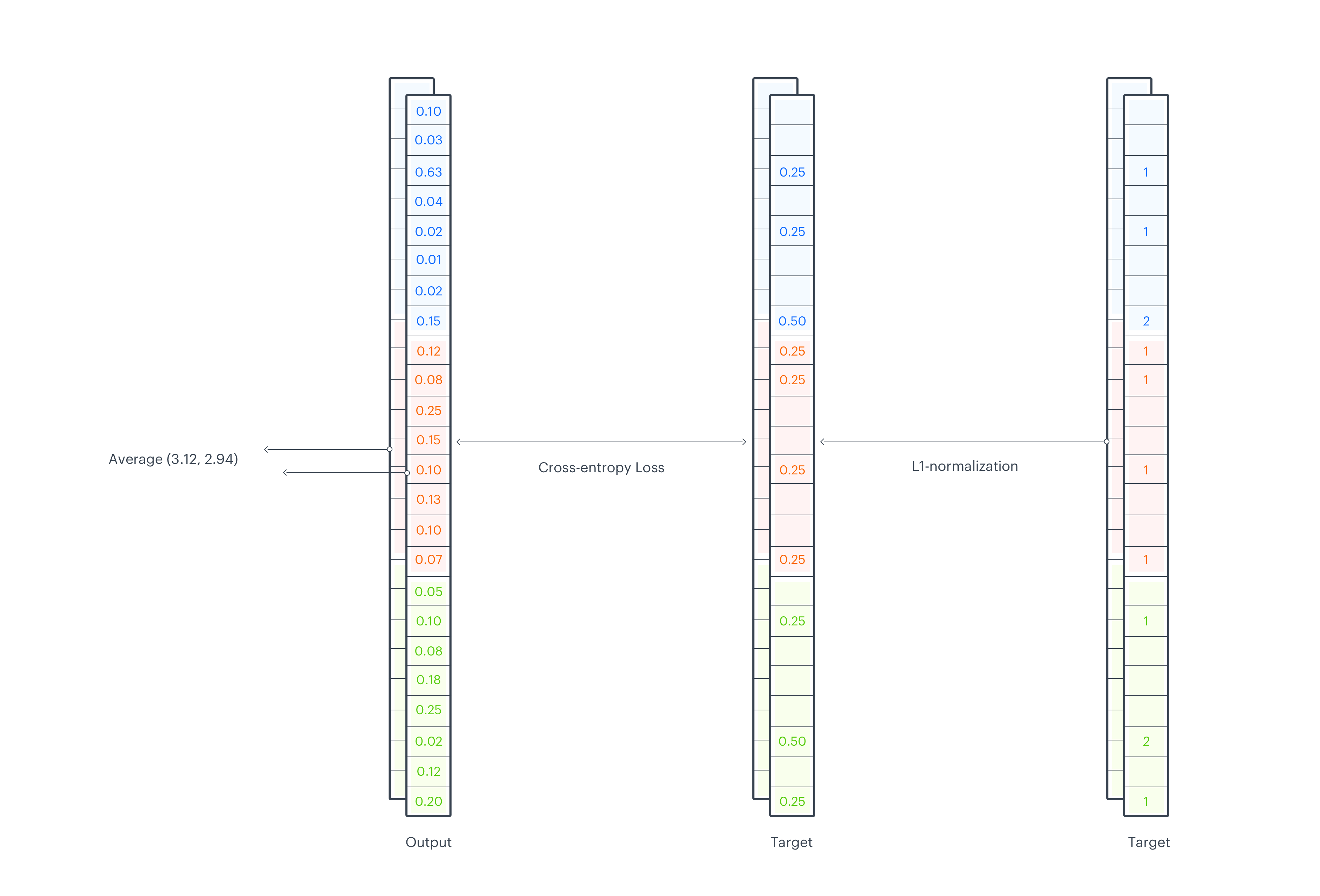
Loss function
To calculate the loss, first we need to L1-normalize the target sketch, which then can be considered as a probability mass function of a discrete distribution. Next, we apply the softmax function on output logits and calculate cross entropy loss between an output and the target. All operations are done across sketch_width, so we end up with a separate loss value for each sketch_depth dimension. In the last step, we average them across depth.
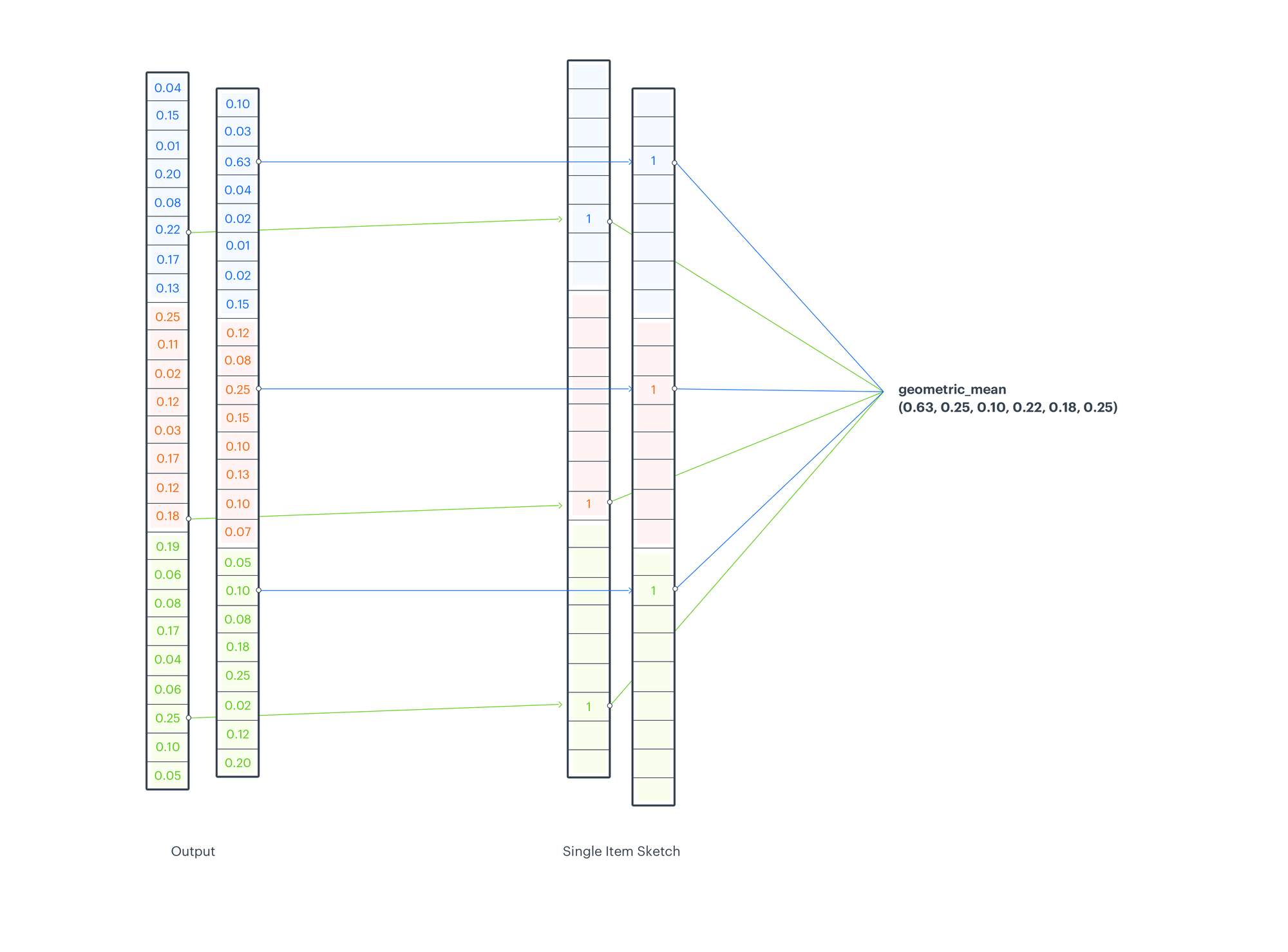
Prediction
To calculate a score for a recommendation candidate we look up scores from relevant indices of model output. For each depth-level and input type we consider recommendation candidate code (representing the manifold region, that the candidate falls into) and we take the score from the output sketch, which was returned for a given code (sketch index). We aggregate them using a geometric mean. The aggregation function differs from the one used in CMS (minimum operation), but while CMS operates on counts, EMDE at this point operates on probabilities.
This way we can create very powerful aggregated data “histograms” encoded in sketches and use them to train a simple neural network. The aim of the model training is to map the regions of an input manifold to the regions of an output manifold. Map user preferences to the probability of the next bought object. What is worth noticing, with only one linear layer and no additional non-linearity, we are able to perform a very non-linear mapping between manifolds. This brings a shift in a current paradigm, where a lot of improvements – various initialization methods or residual connections, which are meant to facilitate NN training, make the overall system closer to a linear transformation.
To validate our approach and get the idea about the EMDE performance in comparison with other methods we took part in several competitions: KDD Cup 2021, Twitter RecSys Challenge 2021, WSDM Booking.com Challenge 2021, SIGIR Rakuten Challenge 2020. We faced multiple different tasks like route prediction, tweets recommendations, scientific papers classification, cross-modal retrieval, and various types of data like text, graph, image. The more in-depth description of our competition efforts can be found here. In each of this tasks, we managed to provide the top solution with considerably lower resources and time required to train and use a model than our opponents.
