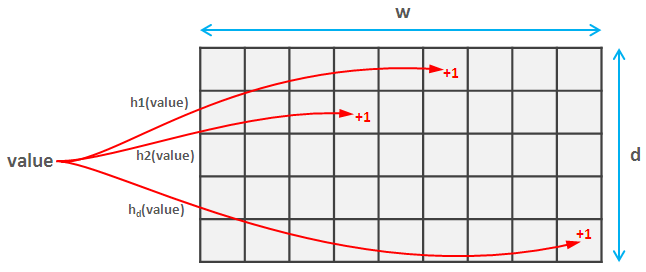
Efficient integer pair hashing

In data science, we sometimes need to calculate hash functions of unsigned 32-bit integer tuples. This need can arise in simple use cases such as efficient pairs counting, but also in approximate data structures which require fast hashing. Such data structures provide a tradeoff between accuracy and speed/memory storage: they produce an approximation of the correct answer, where 100% accuracy is sacrificed for the sake of efficiency. One example is a Bloom filter which is a space-efficient data structure solving the approximate set membership problem (testing whether an element is a member of a set). The Bloom filter is a bit array with multiple hash functions that map elements from the set to the positions in the array. If at least one of the positions to which an element is mapped is empty, we can be sure that that element is not contained in the set. However, when all the positions are occupied, we can only say that an element is in the set with certain probability. This probability depends on the number of hash functions and the number of bits in the array. Bloom filters have many applications such as weak password detection, Bitcoin wallet synchronization, or cyber security. In recommendations, we may use a Bloom filter to remove the items from the recommender system results based on predefined conditions. For example, Medium uses bloom filters to remove already seen posts from the posts recommended to users.

Yet another approximate data structure is a “count sketch” which is used to estimate the number of items in a stream. If a Bloom filter is an approximate “set”, the count sketch can be thought of as an approximate “counting dictionary”. It is based on a family of pairwise-independent hash functions, which are used to map items to sketch buckets and store a count of items assigned to each bucket. Based on this we may then estimate the number of occurrences of a given item. This is a kind of dimensionality reduction where we have a fixed-size space-efficient structure instead of storing the count for each item explicitly. However, it comes as a tradeoff for possibly less accurate results. Count sketches are useful for fast computation in large-scale data analysis. In recommendations, we may use this structure to find popular products – the product page with the highest hit rate.

Usually, to hash a set of integer tuples one would probably start with some standard hash function just to realize how inefficient it is and look for a more performant implementations. In this post we show how to combine two awesome tricks to calculate a very fast unsigned integer tuple hash in pure Numpy, using vectorized operations.

But first, we need to introduce the idea of a pairing function. Pairing functions are used to assign a single unique integer to a pair of non-negative integers. This means that each pair can be mapped to a single integer and there are no two pairs for which function have the same value. If we think of an integer pair as point coordinates in 2-d space, the pairing function finds one coordinate uniquely for each point.

One example of such function is Cantor’s pairing:

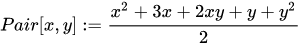
If we visualize it, we can see that this function assigns consecutive numbers to points along diagonals:

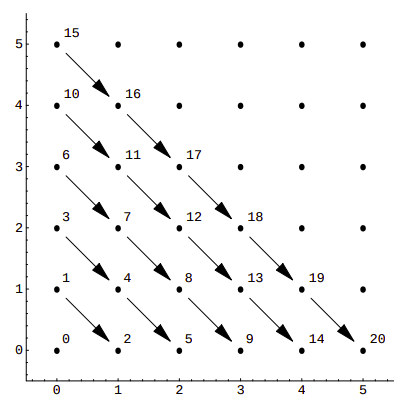
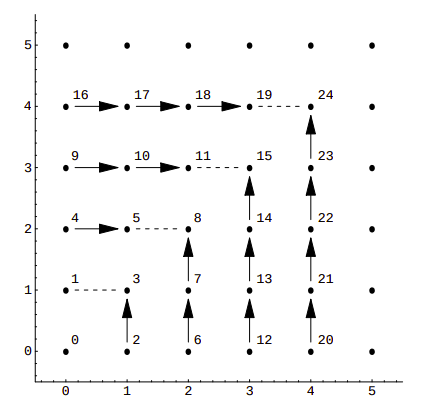
This is a rather simple example, with sub-optimal packing efficiency. If we consider all 100 possible combinations of pairs of numbers from 0 to 9 Cantor’s pairing needs the first 200 numbers to hash them, as CantorPair(9, 9) value is 200.  A more efficient example is Szudzik’s pairing:

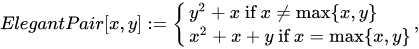
In this case, consecutive numbers are assigned to the points along the edges of a square:

With Szudziks's pairing, we obtain maximum packing efficiency, as the value of SzudzikPair(9, 9) is 99. Performance-wise both functions are similar, with Szudzik’s pair function having a small advantage over Cantor’s.

Here is a Python code example with Szudzik’s pair function implementation using Numpy:

import numpy as np

def szudzik_encode(a, b):
    mask = a >= b
    target = np.zeros_like(a, dtype=np.uint64)
    target[mask] = a[mask] * a[mask] + a[mask] + b[mask]
    target[~mask] = a[~mask] + b[~mask] * b[~mask]
    return target

We compared Szudzik’s pairing with the Python native hash function. As default hashing in Python does not work on Numpy arrays or lists, we need to convert the arrays to tuples:

def naive_hash_pairs(target):
    return np.array([hash(tuple(x)) for x in target])

We generated 10 000 000 pairs of integers from 0 to 2^32-1 and measured the time it takes to create hash codes for all these pairs:

targets = np.random.randint(0, 2 ** 32 - 1, size=(10_000_000,2), dtype=np.uint32)

start = datetime.now()
naive_hash_pairs(targets)
print(f"Naive hash function: {datetime.now()-start}")

start = datetime.now()
szudzik_encode(targets[:, 0], targets[:, 1])
print(f"Szudzik's pair function: {datetime.now()-start}")

Naive hash function: 0:00:17.074799
Szudzik's pair function: 0:00:00.826489

The results show that Szudzik’s pair function is around 20 times faster than default Python hashing, which already is a great improvement.

As mentioned before, in the case of Bloom filters or count sketches, we need multiple hash functions. Since Szudzik’s pairing returns uint64 numbers, to fulfill this requirement we can use a proper hash function which accepts a seed parameter, e.g. xxhash64. Most hashing functions don't take raw ints/uints - they take bytes, so first, we need to pack the uints into byte arrays. Also, to compare it with naive solution, we treat the seed as an additional 3rd element of a tuple, as Python native hash function does not allow a seed parameter.

def naive_hash_pairs_seeded(target, seed):
    return np.array([hash(tuple(x+seed)) for x in target])

def fast_hash(target, seed):
    return xxhash.xxh64(struct.pack('<Q', target), seed=seed).intdigest()

targets = np.random.randint(0, 2 ** 32 - 1, size=(10_000_000,2), dtype=np.uint32)

start = datetime.now()
naive_hash_pairs_seeded(targets, 52)
print(f"Naive hash function seeded: {datetime.now()-start}")

start = datetime.now()
target = szudzik_encode(x, y)
np.array([fast_hash(x, seed=52) for x in target])
print(f"Szudzik's pair function + xxhash: {datetime.now()-start}")

Naive hash function seeded: 0:00:36.409257
Szudzik's pair function + xxhash: 0:00:14.948537

We can see that adding xxhash increased processing time significantly. It is better than the naive Python version, but still very slow.
Let's try some bitwise hashing magic instead. We use Splitmix64 algorithm, which is pseudo random number generator. To explain what pseudo-random numbers are, we must first understand that randomness is not a feature of a single number but rather of a sequence of numbers. It means that sequence elements cannot be reasonably predicted, as they are generated in an indeterministic way. Pseudo-random numbers generator can produce a sequence of numbers that approximates a random number sequence. They have many statistical features associated with random sequences but are produced by a deterministic process. This means that a pseudo-random number generator with a given initial state, a seed, will always generate the same sequence. Such generators are used in many applications, from cryptography to gambling. In AI we often use random numbers to initialize ML model weights or shuffle training data. That is also where the deterministic nature of pseudo-randomness comes in handy as setting a specific seed enables results reproducibility.

Splitmix64 is a pseudo-random number generator, which uses a simple yet very fast algorithm. It keeps 64 bits of state and performs a bit-wise operation to return 64 bits random data.  First, the state is multiplied by a seed value. Next, the state is xor-ed with the state right bit shifted by a specified number of positions. Finally, it is multiplied by a constant. This operation is repeated with a different number of positions to be shifted.

Here we provide a code example of Splitmix64 implementation in Python:

def splitmix64(target, seed):
    out = target.copy()
    SP_STEP = np.uint64(0x9E3779B97F4A7C15)
    out = (out + np.uint64(seed) * SP_STEP)
    out ^= out >> 30
    out *= np.uint64(0xBF58476D1CE4E5B9)
    out ^= out >> 27
    out *= np.uint64(0x94D049BB133111EB)
    out ^= out >> 31
    return out    

targets = np.random.randint(0, 2 ** 32 - 1, size=(10_000_000,2), dtype=np.uint32)

start = datetime.now()
target = szudzik_encode(targets[:, 0], [:, 1])
splitmix64(target, seed=52)
print(f"Szudzik's pair function + Splitmix64: {datetime.now()-start}")

Szudzik's pair function + Splitmix64: 0:00:00.999224

Solution using Splitmix64 algorithm is around 15 times faster than the example with xxhash and the time of computation is clearly dominated by Szudzik's pairing. What if we discard mathematical elegance and generality for a while.. and just approach the problem from a low-level perspective?

Let's do some more bitwise operations:

def bitwise_encode(a, b):
    return (a.astype(np.uint64) << 32) + (b.astype(np.uint64))

targets = np.random.randint(0, 2 ** 32 - 1, size=(10_000_000,2), dtype=np.uint32)

start = datetime.now()
target = bitwise_encode(targets[:, 0], targets[:, 1])
splitmix64(target, seed=52)
print(f"Bitwise encoding + Splitmix64: {datetime.now()-start}")

start = datetime.now()
bitwise_encode(targets[:, 0], targets[:, 1])
print(f"Bitwise encoding: {datetime.now()-start}")

Bitwise encoding: 0:00:00.084675
Bitwise encoding + Splitmix64: 0:00:00.244800

Using bitwise encoding we ended up with super fast solution. Szudzik's Pairing has some other great properties, e.g. keeping the outputs small if the inputs are small, while bitwise coding will always return huge numbers (2^32 or larger). But having this in mind we are now able to choose efficient pair hashing algorithm best suited for our needs.

We utilize these methods in our graph embedding algorithm Cleora. Cleora operates on graphs consisting of nodes which represent some real-life entities and edges that represent relations between them. To use information stored in the graph for some machine learning applications, we need to create vector representations for graph nodes. A detailed description of the algorithm can be found in this post. Here, we will mention the initial step – co-occurrence matrix creation. To generate node embeddings, we first need to store, in a numerical matrix, information about edges between all pairs of nodes. This kind of representation is usually sparse as only some of the nodes are connected with an edge. To increase algorithm efficiency, we keep only coordinates and values of node pairs that are connected with at least one edge. Coordinates are hashed using Szudzik’s pairing and the values for each pair of nodes are efficiently stored for fast retrieval.

These two enhancements to standard hash functions are easy to implement using Numpy and at the same time can drastically improve performance. We are happy to share our tricks and hope it will inspire you to look beyond the obvious paths as the reward can be very satisfying.