EMDE vs Multiresolution Hash Encoding

When we created our EMDE algorithm we primarily had in mind the domain of behavioral profiling. For this reason, we were looking for a method to aggregate multiple events represented by various types of embeddings. However recently, a similar method was developed in the visual domain for two-dimensional data. Researchers from NVIDIA created an input processing method, that significantly lowered training time for Neural Graphic Primitives. We want to compare these two solutions and show how EMDE can be thought of as a solution that has the benefits of multiresolution hash encoding but can be used on high-dimensional data.
Neural Graphic Primitives
Neural graphic primitives are objects represented by a neural network with respect to a given feature. One example is a network that maps from pixel coordinates to RGB colors. This kind of network can learn an image, that will be encoded in its internal structure and can be recreated by querying the network for the subsequent pixels. As representing a single image by a neural network may seem trivial, in fact, this is a highly powerful method. It is used in the neural gigapixel task to approximate a high-resolution picture with billions of pixels. It helps to store detailed image efficiently. However, the difficulty of this task is capturing all details of a picture.
Similarly, we can think of mapping 3D pixel coordinates to the distance to a 2D surface of an object. The distance is positive on the outside of the surface and negative on the inside. The surface is defined where the function is equal to zero. This task is helpful in 3D modeling, video games, simulation, or path planning.
Another interesting example is Neural Radiance and Density Field (NeRF) where based on coordinates in 3D space and view direction a neural net learns to output color and density. It can be used to reconstruct object shape and appearance from a set of 2D photographs with known camera angles.
Neural nets can also be trained for real-time ray tracing in the Neural Radiance Caching task. By tracing small batches of paths of light, the network learns to generalize the radiance throughout the scene.
Multiresolution Hash Encoding
In the paper Instant Neural Graphics Primitives with a Multiresolution Hash Encoding, NVIDIA introduced a method that enables real-time training of neural graphic primitives without compromising the quality of the results. This gained a huge interest in the research community, the solution won the best paper award at SIGGRAPH. Also, it was listed as one of TIME’s magazine best inventions of 2022.

The idea introduced in this paper is to create input data encoding that can facilitate training procedure for neural graphic primitives. In the first step, multiple grids of increasing resolution are created. The number of separate grids is controlled by the number of levels L parameter. The resolution growth factor (b) is calculated based on the minimum (Nmin) and maximum (Nmax) resolution and the number of levels according to the provided formula:
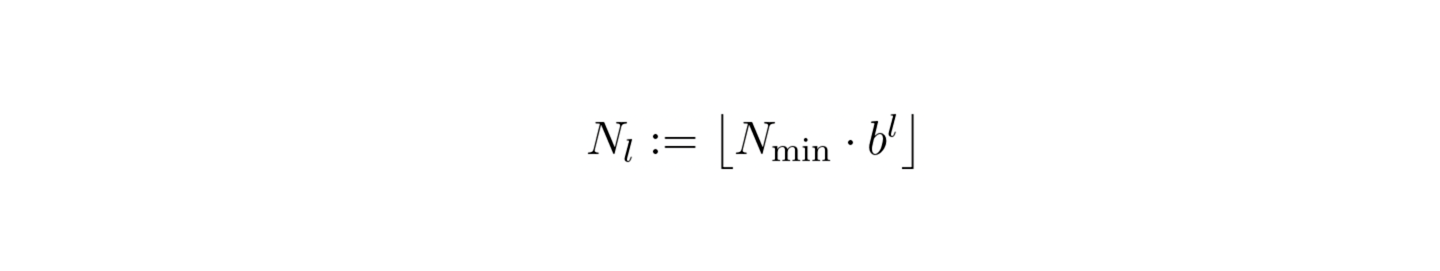
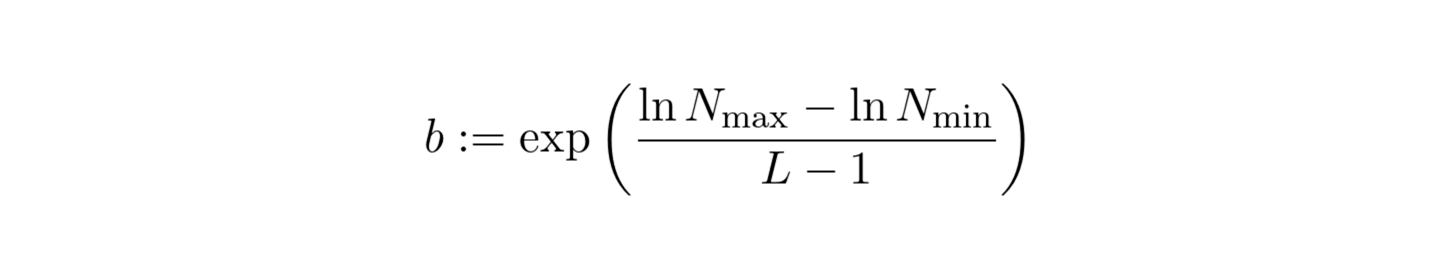
Given coordinate x, on each level, we scale x by the resolution on this level and round up or down to find the relevant cell:
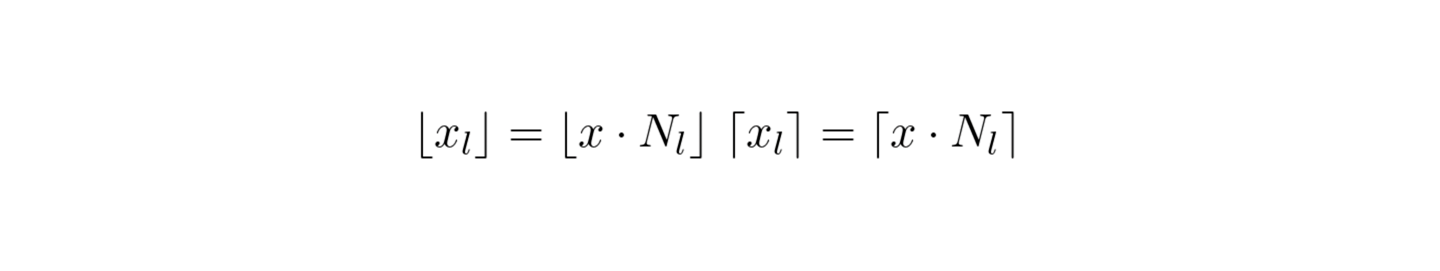
In the next step, cell corner coordinates are mapped to a feature vector array specified for each level. The size of an array is fixed and governed by the hyperparameter T. Another configurable parameter is the number of dimensions per entry. For a coarse grid that requires less than T parameters, there is 1:1 mapping between corners and array entries. Levels with finer grid use the following hash function to create a mapping:
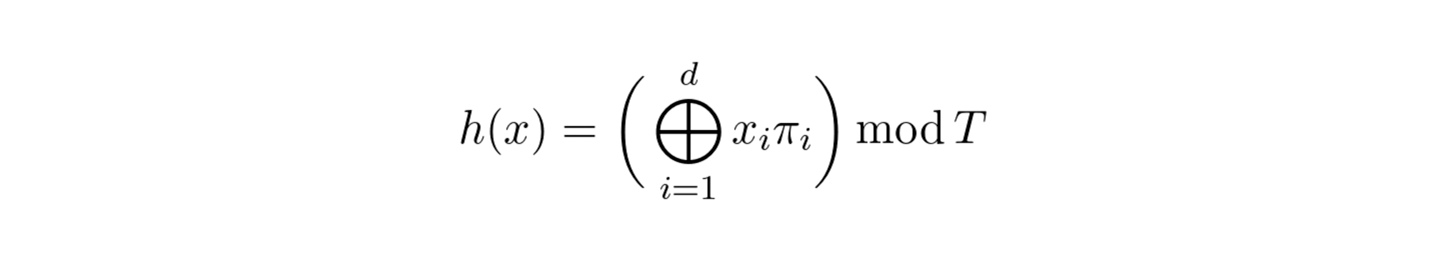
There is no explicit collision handling. Instead, feature vectors are trainable to learn a representation that implicitly handles collisions. However, the size of a feature vector array can’t be too small in which case too many grids will be assigned to the same entry.
To make the optimization of feature vectors feasible, array entries corresponding to a given grid cell are linearly interpolated according to an input position within a grid cell. As the described process takes place independently on each array level, the final input representation is the concatenation of results from each level. This can be enriched with some additional features or serve as a standalone input to a neural network.
Representations created this way are task agnostic, so they are trained to well represent input data independently to a task it will be applied for. Using multiple grids with different resolutions implements varying focus. Finer resolution will help to focus on details, while coarse ones will be responsible for capturing an overall scenery.
Performance
What contributes to multiresolution hash encoding popularity is how it can improve neural graphic primitives training. With provided input encoding, neural graphic primitives can be trained with significantly smaller neural networks. As a result, they can obtain outstanding capabilities of real-time training using only one GPU. What is more, within a given task, results quality is comparable with state-of-the-art methods. At the same time, network can be trained almost 8 times faster than the baseline.

These results can revolutionize many fields where up to this date memory-costly and inefficient methods were predominant.
EMDE
Multiresolution hash encoding was designed to fit low-dimensional data in the image processing domain. What was our conclusion after reading the paper: “Wow! It is like EMDE for visual data.” What we want to show in this post will go the other way round: “Our EMDE algorithm is like multiresolution hash encoding for high-dimensional data.”
As multiresolution hash encoding creates a grid that divides a picture, the EMDE algorithm creates hyperplanes that divide a data manifold. Often in data science, we operate on multidimensional vector representations of some predefined entities, like text embeddings or graph embeddings. We can conceptually represent them as points on a data manifold. In that case, manifold represents all possible entities of a type represented by given embeddings, e.g. all possible words. Vectors similarity will translate into the “closeness” of points on a manifold, e.g. similar words will be placed next to each other on a data manifold.
We then create multiple separate divisions of this manifold, same as multiple grids in NVIDIA proposal. How we create the divisions is where we differ. Instead of a regular grid, we use irregular divisions with hyperplanes that we select with a data-dependent algorithm to avoid creating empty cells. On all levels we use the same resolution, as we obtain different granularity on the intersection of multiple levels thanks to varying irregular divisions. This way we obtain a similar effect to the multi-resolution setting.
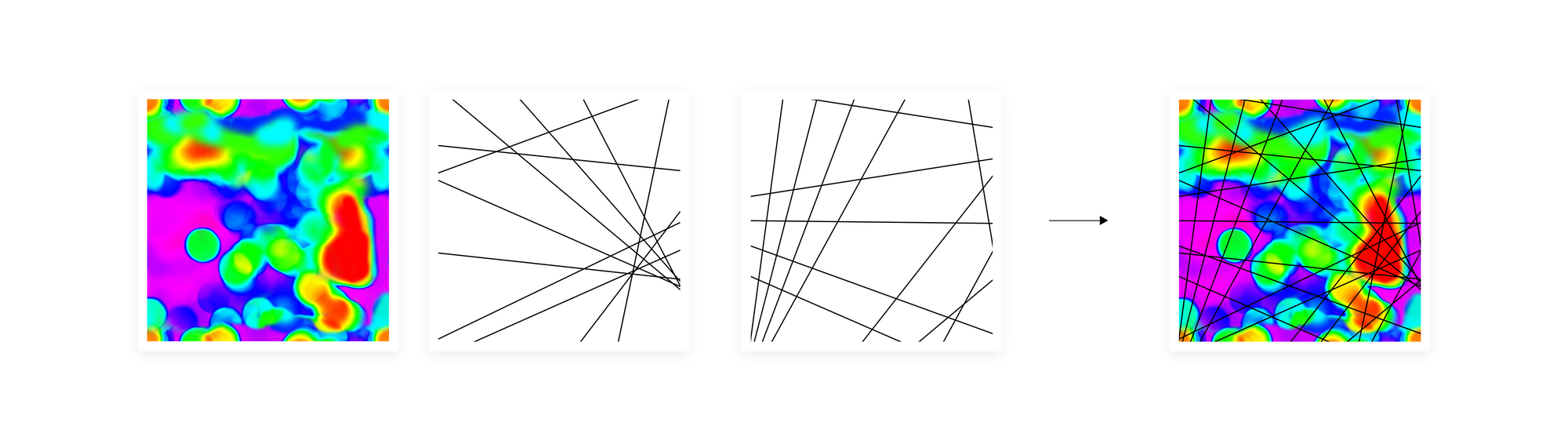
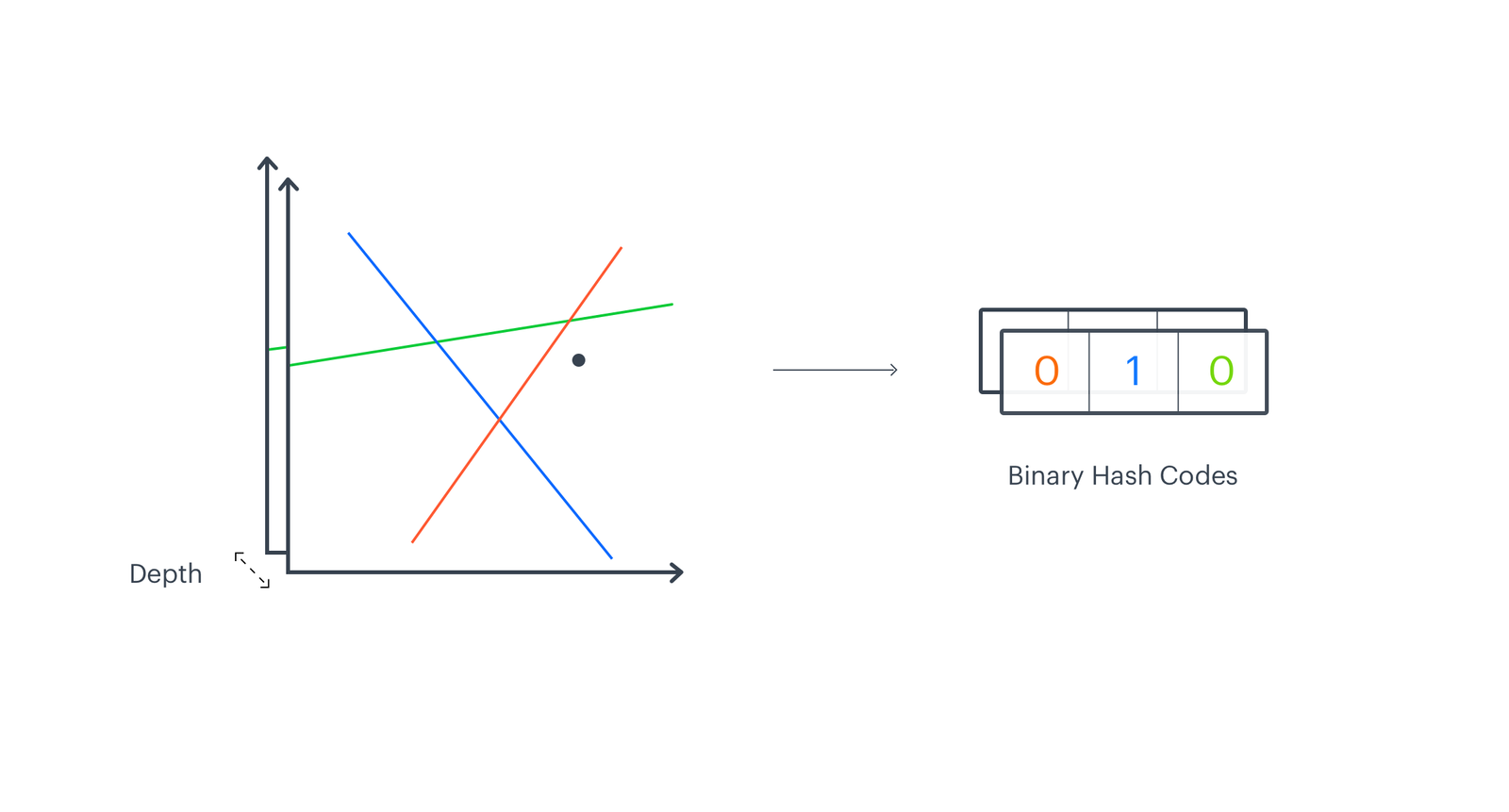
As multiresolution hash encoding finds a voxel with given input coordinates, our algorithm defines a region on a manifold with a selected data point. The difference is that our data points represent high-dimensional vectors. We then map regions on each level to a fixed-size array. Our mapping is based on the position of a vector with respect to a given hyperplane dividing the manifold. We create a binary vector of the same length as the number of hyperplanes K, where each entry states if an input embedding is below or above the hyperplane. We treat it as a K-bit integer and transform to a single code pointing to a region on a manifold. The final representation is created by incrementing the count in entries indexed by relevant code. All the details are described in our previous post EMDE Illustrated.
We use EMDE in behavioral modeling to aggregate many events, like clicks or buys, into a single representation, which serves as an input to a simple neural network trained to predict future behaviors. However, EMDE encoding proved to be effective in many other tasks such as predicting next travel destination, graph node classification, or cross-modal retrieval. Whenever there is a need to aggregate information in a lossless way or transform high-dimensional feature space into fixed-size representation, EMDE can be of help.
EMDE and Multiresolution Hash Encoding face to face
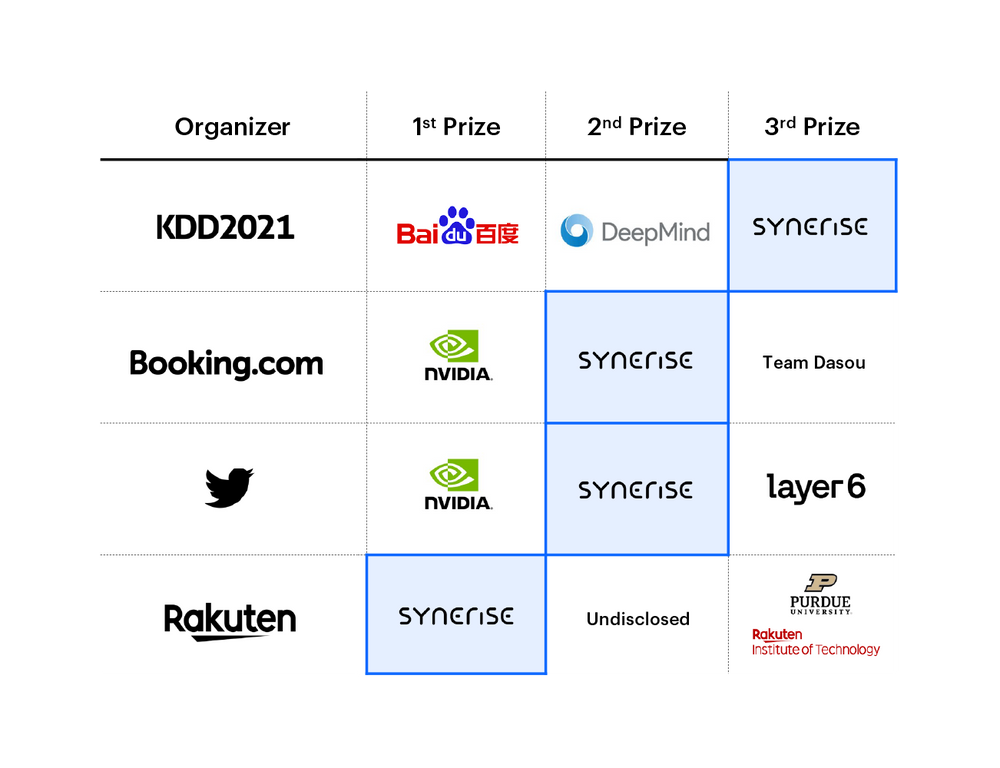
Similar to multiresolution hash encoding, EMDE significantly increases model performance. The effort that was put into creating input data representation pays off in radically smaller models and shorter training time. In most of our use cases, we use a sparse feed-forward network with around 5 layers and trained for 2 to 5 epochs on a single GPU. At the same time, we don't compromise the quality, which we proved in the competition where we battel tested our solution.
However, the starting points of these two methods were different. Multiresolution hashing was made to work with visual data. For higher dimensional data, an issue will arise as the number of voxels will grow drastically with the number of dimensions (Nld), and for each voxel, the number of corners equals 2d. This way of defining voxels works well for smaller dimensions like 2d or 3d objects, but in higher dimensional space creating meaningful encoding becomes infeasible.
In the case of multiresolution hash encoding, the size T of a hash table is where the memory consumption is traded for performance. The growing number of input dimensions requires an increase in T for implicit collision handling to work. For higher dimensions, the hash table size would explode, or other way it would result in too many collisions.
EMDE was created to work with high-dimensional data in the first place. The
number of separate regions is independent of the number of dimensions of input space and is the same on each level – 2K. We usually set the number of hyperplanes K to 16, so each region is defined as a 16-bit integer, which corresponds to the array entry of the final encoding.
Comparing these two methods, we can see that seemingly distant issues can result in similar ideas. Discussed solutions differ in aspects that allow them to be applied in different scenarios but carry the same benefits of lifting weight from the model itself to input encoding.
